Economic inclusion
Annex 5.2 Assumptions underlying inclusion gap calculations
- Details
- Economic inclusion
This annex provides further background information on how the indicators described in Tables 5.1, 5.3 and 5.5 were translated into gender, youth and regional inclusion gaps. Full details and the underlying data are available online in downloadable Excel files.
For the gender and youth gaps, the data took three forms:
- policy indices constructed by organisations such as the EIU, the World Bank, the International Labour Organization and the World Economic Forum;
- plain data – for example, test score data from PISA (the Programme for International Student Assessment) or, for countries where PISA data are not available, TIMSS (the Trends in International Mathematics and Science Study);1
- data expressing a ratio, percentage difference or absolute difference (in percentage points) between the target group (women or 15 to 24-year-olds) and a comparator group (men or 25 to 64-year-olds respectively).
Policy indices incorporate a normative interpretation, typically running from a worst value of n to a best value of N in integer steps. The data analysis underlying the gap calculations generally sought to maintain that interpretation. Hence, the only manipulation of these data was their mapping to the transition indicator scale, which starts with a jump from 1 (the lowest possible value, equivalent to a country before the beginning of transition) to 2- (12/3) and subsequently increases linearly until it reaches 4+ (41/3). If k denotes the index value, assumed to be an integer, n <_ k <_ N, and x denotes the transformed index on the transition indicator scale, the following formulas were used:2
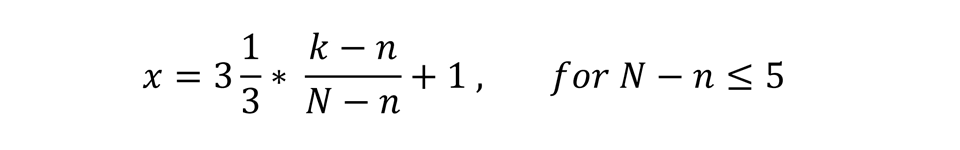
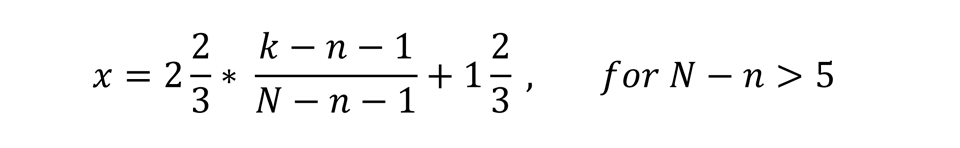
These formulas ensure that the transition indicator value assigned to the lowest index value is always 1 and that the next value is at least 2-. The remainder of the index values are mapped proportionally to the interval between 2- and 4+.
Plain data and data expressing differences were mapped into the transition indicator scale in discrete (1/3) steps, using the cut-offs defined in Table A.5.2.1. The cut-offs were set either in relation to international best and worst practices, or using some combination of best or worst practices and a normative judgement – as in the case of gender gaps, where only parity between males and females was good enough to earn the highest possible score of 4+ on the transition indicator scale, a situation that exists internationally for some indicators (for example, access to education), but not for many others at present for example, gender pay gaps continue to exist everywhere.
After expressing all data on the 1 to 4+ transition scale, the transformed data were averaged within each category. In the gender gap analysis, which in some categories involved a large number of series with overlapping information content, this was done using a principal components methodology that assigns weights in relation to the new information carried by each series. In the youth gap analysis, simple averages were used – except in the case of the quality of education dimension, where a weighted average was applied.3
The regional gap analysis was based on two measures: Gini coefficients based on means of PSU (regional-level) data, and the percentage difference between the top and bottom quintiles of regions. Hence, both measures are defined as continuous indices between 0 and 1. For each of these indices, a lower (n) and upper cut-off (N) were chosen, based on international comparisons. Between these extremes, the following formula was used:
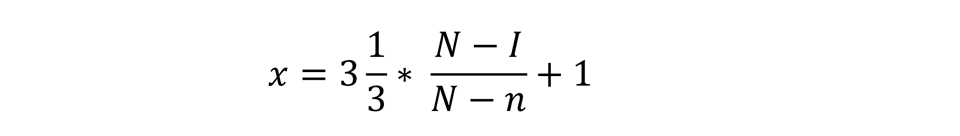
The lower and upper bounds are defined in Table A.5.2.2.
For each dimension, the resulting two indices were subsequently averaged and translated into "negligible", "small", "medium" or "large" gaps.
- Gaps in the PISA scores were filled by running a linear regression of PISA scores on TIMSS scores using data from countries where both are available, and using the estimated regression coefficients to fit PISA scores for countries where only TIMSS data were available. [back]
- An exception was made in the case of three indices (for labour market flexibility and perceptions of educational quality) produced by the World Economic Forum (see Table 5.2). Those indices run from 1 to 7, but no country was rated higher than a 6. In this case, the scale was truncated from 7 to 6 to allow a more generous definition of a "negligible" gap. [back]
- First, a combined "school reliability" score was calculated as a simple average of the teacher shortage, material shortage and school accountability scores. Second, a weighted average was calculated with weights in the following proportions: test scores 1, school reliability 1, business executives' perception of quality World Economic Forum (WEF) 1.5, households' perception of quality (LiTS) 0.5, and university rankings 1.5. [back]